Laplace-Domain Crosstalk-Free Source-Encoded
Elastic Full Waveform Inversion Using Time-Domain Solvers
Geophysics, 2024
- Zhaolun Liu Saudi Aramco
- Jürgen Hoffmann DNO ASA
- Etienne Bachmann Princeton University
- Congyue Cui Princeton University
- Frederik J. Simons Princeton University
- Jeroen Tromp Princeton University
Objectives
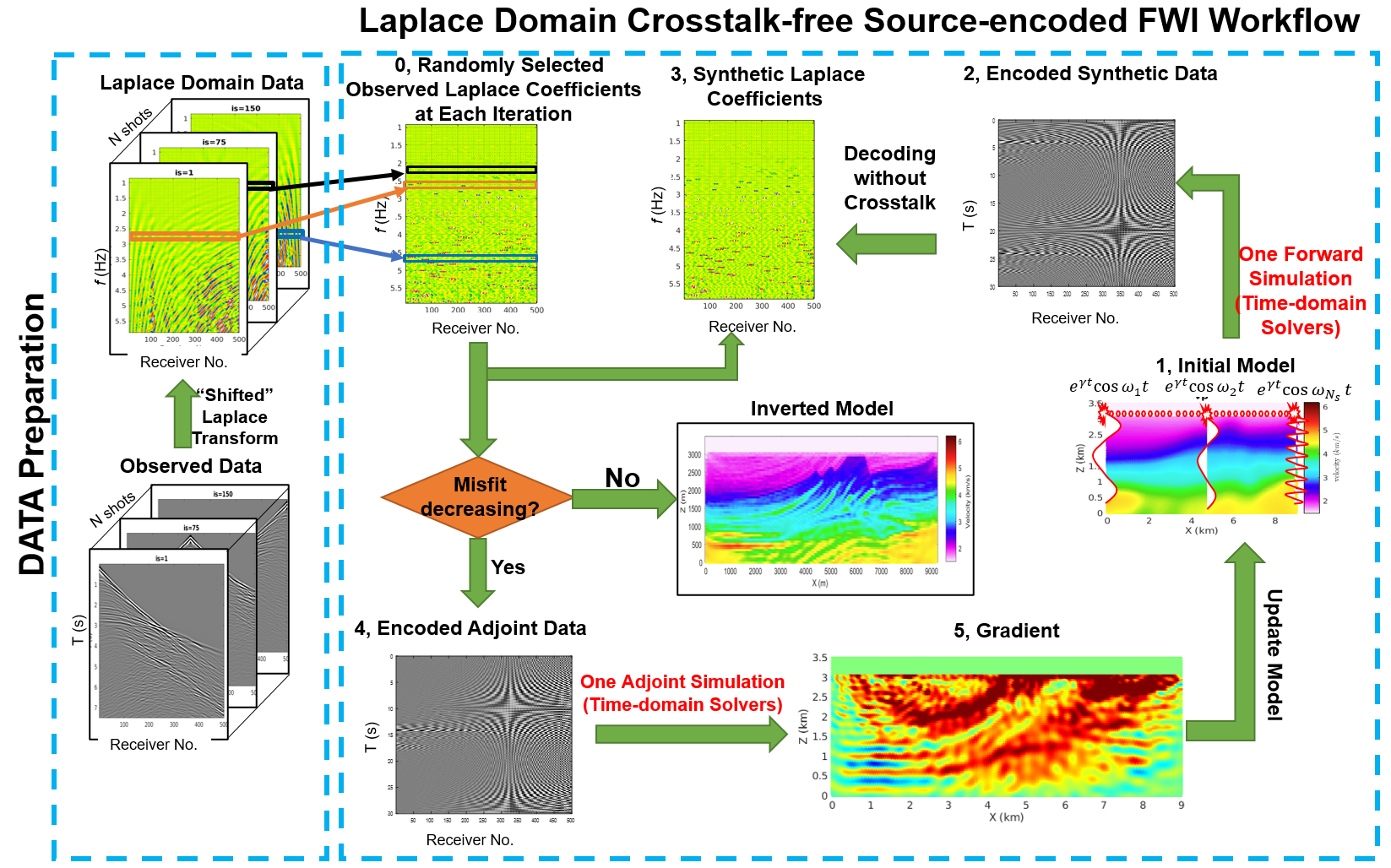
To reduce the computational time of elastic full-waveform inversion (FWI) using time-domain solvers, we develop a new version of source encoding that (1)~only needs two numerical simulations per iteration, namely, one source-encoded forward simulation and one source-encoded adjoint simulation, (2)~will not generate any cross-talk noise, (3)~poses no restriction on acquisition geometry, e.g., a fixed receiver spread for random polarity encodings or a dense source array for plane wave encodings, and (4)~can easily implement time windowing.
Methods
We present a new version of Laplace-domain crosstalk-free source encoding for elastic full-waveform inversion (FWI) using time-domain solvers. As shown in Fig.1, our method of source-encoding for FWI assigns to each source at random for each iteration a unique complex frequency, introducing a damping factor to take care of attenuating late arrivals. The misfit criterion is the sum of the squared errors in the ``shifted'' Laplace coefficients between observed and synthetic data. Additionally, we derive a phase-only misfit. The source-time function takes the form of a weighted cosine or sine with exponentially increasing amplitude. We simultaneously activate all the sources and carry out one source-encoded forward simulation followed by one source-encoded adjoint simulation, using a time-domain solver. The encoded forward and adjoint wavefields are run until they reach steady state. The gradient is calculated through zero-lag cross-correlation between the steady-state encoded forward and adjoint wavefields over a time period proportional to the inverse of the encoded frequency spacing. Owing to the orthogonality between the trigonometric terms of the encoding operator, no crosstalk is introduced during gradient calculation, and there are no limitations on acquisition geometry. By tuning the damping factor, we can time-window the data even when only one or a few sparse frequencies are being sampled. Time-windowing allows for the selection of specific arrivals during the various stages of the inversion.
Results
We demonstrate the effectiveness of our multi-bin WD algorithm by applying it to invert shingling events (see Fig. 1c) from a complex layered model (see Fig. 1a). The near-surface model inverted by multi-bin WD is close to the true model (see Fig. 1g), and the travel time, waveform, and dispersion curves of the synthetic data calculated from the inverted model by multi-bin WD match well with those from the observed model (see Figs. 1h-1i). In comparison, wave-equation traveltime inversion (WT, see Figs. 1d-1f) can only update the model (see Figs. 1d) to match the travel time of the data (see Fig. 1e), but the waveform and dispersion curves of the synthetic data from WT are still discrepant with the observed ones. Next, we apply multi-bin WD to invert surface waves for S-wave wave speed (VS) (see Fig. 2). The seismic data set is collected in Wyoming, US for the critical zone study (see Fig. 2a). Eight bins are used, and the corresponding dispersion curves are calculated (see Fig. 2b) and used to invert for the VS model. The initial and inverted VS model are shown in Figs. 2c and 2d. The waveform comparison before and after inversion is shown in Figs. 2e and 2f, respectively. We can see that the waveform matches very well after multi-bin inversion, even though our misfit is based on the dispersion curves. These results demonstrate the effectiveness of the multi-bin WD method.
